クリープとは、
物体に一定の外力を与えることによってひずみ(変形)が進行する過程をいう。

応力緩和とは、
物体に一定のひずみを与えることによって生じた応力が低下する過程をいう。

※ひずみ＝変形量/原形量　(本講座１．粘弾性とは　図２参照)　

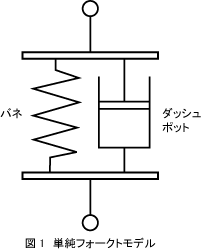図１は、弾性のバネと粘性のダッシュポット(内部の板を上昇させる際に液体が抵抗する)が並列につながった状態で 上下の両端を一定の力で引っ張るとそれぞれ均等に伸びが生じる力学的模型である。　

1. バネ(弾性)だけを一定の力で引っ張ると瞬時に伸びが生じる。
2. ダッシュポット(粘性)だけを一定の力で引っ張ると瞬時には伸びず、時間経過に伴い伸びが進行する。

右のモデルの両端を一定の力で引っ張るとバネは瞬時に伸びるところ、ダッシュポットの影響により双方同じ速さで伸びが進行する。

一方ダッシュポットは伸びの進行が続く途中、バネの影響(ある程度伸びたバネの力)により進行が止まる。

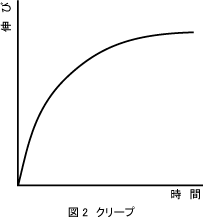図２は、単純フォークトモデルの両端を一定の力で引っ張った直後から伸びが生じる過程(伸びと時間の関係)である。
同図はモデル全体に与える力が一定の間、時間経過に伴い伸びが進行する粘性(伸びの速度が低下するのは弾性の影響)と伸びの進行が止まる弾性(瞬時に伸びないのは粘性の影響)の共存、すなわち粘弾性のクリープ曲線である。

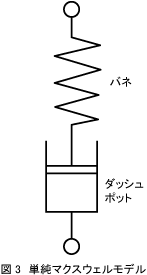図３は、弾性のバネと粘性のダッシュポットが縦列につながった状態で上下の両端を一定の伸びで保持するとそれぞれ均等に応力が生じる力学的模型である。

1. バネ(弾性)だけを一定の伸びで保持すると応力も一定のまま変わらない。
2. ダッシュポット(粘性)だけを一定の伸びで保持すると応力は0のまま変わらない。

右のモデルの両端を一定の伸びで保持するとバネは瞬時に同じ変形量まで伸び(弾性)、ダッシュポットはその瞬間伸びない(粘性)。 時間経過に伴い伸びたバネは自身の応力で原形へ戻り始め、ダッシュポットはその力で伸び(中の板が上昇し)始める。 バネが原形量まで戻ると応力は0になり、ダッシュポットの伸びも進行が止まる。

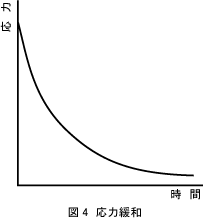図４は、単純マクスウェルモデルの両端を伸ばした直後からその伸びを保持している間に応力が低下する過程(応力と時間の関係)である。
同図はモデル全体に与える伸びが一定の間、時間経過に伴い応力が連続的に低下する粘性挙動(弾性の影響で応力0ではない)と 応力が生じている弾性挙動(粘性の影響で応力一定ではない)の共存、すなわち粘弾性の応力緩和曲線である。

［参考文献］
1.やさしいレオロジー
    (産業図書発行　村上 謙吉　著)
    第六章　典型的な粘弾性変形