遅延時間とは、
物体に一定の外力を与えるとひずみ(変形)が進行する過程(クリープ)において特定のひずみに到達したときの経過時間をいう。

緩和時間とは、
物体に一定のひずみを与えると応力が低下する過程(応力緩和)において特定の応力に到達したときのの経過時間をいう。
＊ひずみ＝変形量/原形量　(本講座１．粘弾性とは　図２参照)
＊クリープと応力緩和　　(本講座２．クリープと応力緩和参照)

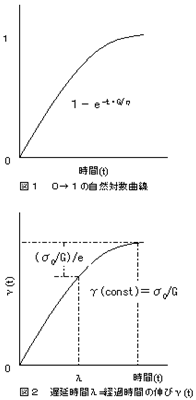粘弾性体を一定の力で引っ張ると、ある速度で伸びが進行する粘性に対して、ある程度伸びるとそれ以上進行しない弾性が相互に作用して、伸びは減速して進行がとまることを前節(２．クリープと応力緩和　1．粘弾性のクリープ)で述べた。
時間関数である伸びをγ(time)とすると、伸び(ひずみ)が進行するクリープは減速しながら曲線を描いて一定伸びγ(const)に到達する。両者間に次の関係がある。
γ(t)＝γ(const)－(σ₀/G)ｅ^－t・G/η＝σ₀/G(１－ｅ^－t・G/η)
γ(const)＝σ₀/G
t：time≧0　σ₀：一定の力　Ｇ：弾性率　η：粘性率
１－ｅ^－t・G/η：０から１に至る自然対数曲線　(図１)
ここで、特定時間λを考え、λ＝η/Gとすると、t＝λの場合、
γ(t)＝σ₀/G(１－ｅ^－1)＝σ₀/G(１－1/ｅ)　(図２)

この特定時間λを遅延時間という。
経過時間が遅延時間λのとき、物体の粘性と弾性の比は伸びの進行が停止するまで一定伸びγ(const)の1/e倍(×100％)という定数できまる。(e：2.718：自然対数の底)
遅延時間λ(=η/G)が大きいほど粘性の寄与が大きい(物体が伸びにくい)。あるいは弾性の寄与が小さい粘弾性物体である。

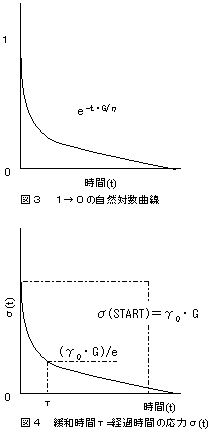粘弾性体を一定の伸びで引っ張ると、応力が一定のまま変わらない弾性に対して、伸びが止まると応力は0のまま変わらない粘性が相互に作用(弾性体が縮む一方で、粘性体が伸びる：単純マクスウェルモデル)して、応力は低下して0になることを前節(２．クリープと応力緩和　２．粘弾性の応力緩和)で述べた。
時間関数である応力をσ(time)とすると、初期応力σ(START)が低下する(物体内部の分子鎖の絡み合いが解れる)緩和は減速しながら曲線を描いて応力0になる。両者間に次の関係がある。
σ(t)＝σ(START)ｅ^－t・G/η＝(γ₀・G)ｅ^－t・G/η
σ(START)＝γ₀・G　　
　t：time≧0　γ₀：一定の伸び　Ｇ：弾性率　η：粘性率
ｅ^－t・G/η：１から０に至る自然対数曲線　(図３)
　ここで、特定時間τを考え、τ＝η/Gとすると、t＝τの場合、σ(t)＝γ₀・G・ｅ^－１＝γ₀・G/ｅ　(図４)　　 　　　　　　　

この特定時間τを緩和時間という。
経過時間が緩和時間τのとき、物体の粘性と弾性の比は応力が0になるまで初期応力σ(START)の1/e倍(×100％)という定数できまる。(e：2.718：自然対数の底)
緩和時間τ(=η/G)が大きいほど粘性の寄与が大きい(粘性体の伸びが遅い)。あるいは弾性の寄与が小さい粘弾性物体である。

［参考文献］
1.　レオロジー入門(工業調査会発行　岡小天　編著)
　　第八章 固体粘弾性

2.　やさしいレオロジー(産業図書発行　村上謙吉　著)
　　第六章 典型的な粘弾性変形

3.　レオロジー基礎論(産業図書発行　村上謙吉　著)
　　第四章　典型的な粘弾性変形