粘弾性物体の応力緩和挙動は、ひずみを与えた瞬間から急激に変化したのち、なだらかに進み、終了に至るまで長い時間を要する。 この急激な変化を捕らえるためには、瞬時にひずみを与え、その瞬間から応力の計測を必要とする。 実用上、0.001秒以下で生じる応力変化や10000秒以上の計測は非現実的である。 応力緩和挙動は一定温度下における測定が基本条件である。粘弾性物体には温度依存性があるので、 応力緩和の測定温度が異なると緩和の速さ(緩和時間)に影響する。 この現象を利用した広いタイムスケールの応力緩和挙動を求める方法が時間－温度換算則である。 これにより求めた応力と時間の関係を合成曲線(マスターカーブ)という。

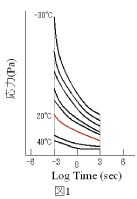図１は粘弾性物体にひずみを与えた応力の連続的な低下を計測する応力緩和測定である。測定時間は0.001から1000秒まで一定温度下で測定する。 応力の一番高い曲線が-30℃、測定温度を10℃間隔で上昇させて測定した曲線が順次下方へ並んでいる。 このグラフから、温度を上昇させると、応力が低下していること、各温度下において時間経過に伴い応力が低下していることがわかる。 温度を上昇させることと時間が経過することの間に“応力が低下している”という共通の現象が生じている。 赤色の曲線は20℃における応力緩和、１本上の曲線は10℃、1本下の曲線は30℃における応力緩和である。  

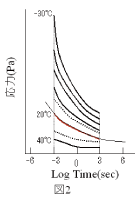図２は、20℃の曲線(赤)の１本上の曲線(10℃)を左(短時間側)へ水平に移動させ、１本下の曲線(30℃)を右(長時間側)へ移動させてそれぞれ20℃の曲線と重ねている。 20℃の曲線の上下点線は、移動前の位置である。このグラフから２本の曲線を左右へ移動させることにより、20℃の応力緩和が測定時間である６桁タイムスケールより短時間側、 長時間側へ広がったことがわかる。10℃の曲線を20℃に置換すると0.001秒より短時間側へ延び、30℃の曲線を20℃に置換すると1000秒より長時間側へ延びた、 この置換を時間－温度換算則という。曲線を移動しない温度(この場合20℃)を基準温度という。時間軸上で延びた関数をシフトファクター(移動因子) logａTという。

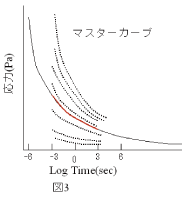 図３は基準温度20℃の曲線(赤)に対して縦に並んだ、測定温度-30℃から40℃まで10℃間隔の曲線を左右に移動しで重ねると１本になった曲線である。 この曲線をマスターカーブ(合成曲線)という。マスターカーブは、この場合、-30℃における10-3secの応力が10-6sec付近へ移動、 40℃における10-3secの応力が106sec以上へ移動しておりその間を他の温度の曲線が移動して１本に重なった形である。 このマスターカーブから、ある粘弾性物体の20℃における応力緩和挙動が本来10-6sec以下～106sec以上という広いタイムスケールであることを予測できる。 実際に広いタイムスケールの応力緩和を測定し、その曲線がマスターカーブに合致するための条件を導いた経験則をＷＬＦ則という。

経験則から粘弾性物体のガラス転移温度から100℃高い温度までにおける応力緩和挙動のマスターカーブは、下記のシフトファクターを適用すると、 ガラス転移温度よりも５０℃高い温度を一定にした広いタイムスケールの応力緩和実測曲線と合致することが知られている。

①ガラス転移温度+50℃を基準温度にしたシフトファクター算出
　　シフトファクター.logａT＝－C1(T－Ts)/(C2＋T－Ts)
　　定数　C1 ：8.86　C2：101.6
　　測定温度　T：ガラス転移温度～100℃
　　基準温度　Ts：ガラス転移温度＋50℃

②ガラス転移温度を基準にしたシフトファクター算出
　　シフトファクター.logａT＝－C’1(T－Tg)/(C’2＋T－Tg)
　　定数　C’1 ：17.44　C’2：51.6
　　測定温度　T：ガラス転移温度～100℃
　　基準温度　Tg：ガラス転移温度

［参考文献］

1. レオロジー入門(工業調査会発行　岡小天　編著)
   第八章 固体粘弾性