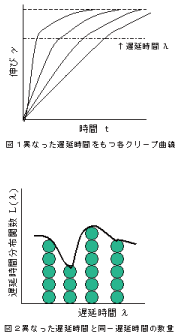
前節（3.遅延時間）では、粘弾性物体の粘度と弾性率が相互作用して、ひとつの特性時間がクリープ曲線から求まると述べた。 これは単純フォークトモデル（弾性部と粘性部を各１個並列配置した模型）を例に挙げ、それが基礎的な粘弾性物体と考えた場合である。（前節2.クリープ参照）

　実際の粘弾性物体における遅延時間は、物体内部における各微細部（単純フォークトモデル）の集合体として現れるものである。 すると図１図２のように各微細部にそれぞれ遅延時間が存在し、微細部間において同一の遅延時間と異なる遅延時間の存在が考えられる。 図２縦軸の遅延時間分布関数Ｌ（λ）は単位応力あたりのひずみ（1/Pa）を次元とする、同一遅延時間における各微細部ひずみの合計である。 横軸の遅延時間は見やすく説明するために、隣どうしに隙間があるが、実際には連続的に分布した曲線を示す。その曲線が遅延スペクトルである。 遅延スペクトルは次に述べる緩和スペクトル同様、粘弾性物体のレオロジー挙動に最も基本的な材料特性関数である。

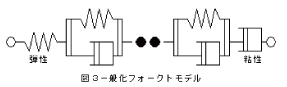　図３の一般化フォークトモデルは弾性部と粘性部各１個の並列配置（単純フォークトモデル）が縦に数多く連結しており、遅延時間が連続的に分布していることを意味する。 また各単純フォークトモデルには同一遅延時間どうしの粘弾性物体内部における微細部が集合していることも含む。 通例として、モデル両端に弾性部と粘性部が連結する。

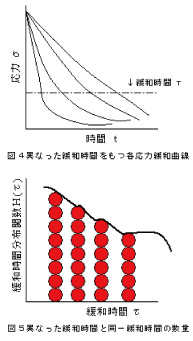前節（3.緩和時間）では、粘弾性物体の粘度と弾性率が相互作用して、ひとつの特性時間が応力緩和曲線から求まると述べた。 これは単純マクスウェルモデル（弾性部と粘性部を各１個縦列配置した模型）を例に挙げ、それが基礎的な粘弾性物体と考えた場合である。（前節2.応力緩和参照）

　実際の粘弾性物体における緩和時間は、物体内部における各微細部（単純マクスウェルモデル）の集合体として現れるものである。 すると図４図５のように各微細部にそれぞれ緩和時間が存在し、微細部間において同一の緩和時間と異なる緩和時間の存在が考えられる。 図５縦軸の緩和時間分布関数Ｈ（τ）は単位ひずみあたりの応力（Pa）を次元とする、同一緩和時間における各微細部応力の合計である。 横軸の緩和時間は見やすく説明するために、隣どうしに隙間があるが、実際には連続的に分布した曲線を示す。その曲線が緩和スペクトルである。 緩和スペクトルは、上述の遅延スペクトル同様、粘弾性物体のレオロジー挙動に最も基本的な材料特性関数である。


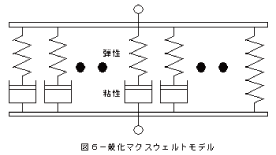　図６の一般化マクスウェルモデルは弾性部と粘性部各１個の縦列配置（単純マクスウェルモデル）が横に数多く連結しており、緩和時間が連続的に分布していることを意味する。 また各単純マクスウェルモデルには同一緩和時間どうしの粘弾性物体内部における微細部が集合していることも含む。 通例として、モデル右端に弾性部が連結する。

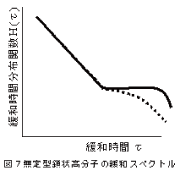
　無定型鎖状高分子の緩和スペクトルは、物質の種類に関係なく図７のように曲線に右下がり傾斜部と平坦部が存在する。 平坦部が長く端の角が鋭いほど、粘弾性物体の分子量が均一であり、平坦部の実線に対して破線部の物体は不均一である。

［参考文献］

1. やさしいレオロジー（産業図書発行　村上謙吉　著）
   第六章　典型的な粘弾性変形
   
   
2. レオロジー入門（工業調査会発行　岡小天　編著）
   第八章　固体粘弾性