固体の弾性の原因をあきらかにするためには、固体をつくっている分子間にはたらく力の性質について知らなくてはならない。
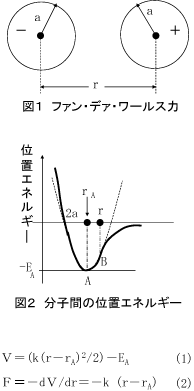
分子間にはたらく力の１つとしてファン・デァ・ワールスの引力というものがある。 いま図１のように半径ａのふたつの分子がたがいに近づくと、 個々の分子運動と相互間の静電誘導のために瞬間的に電気双極子をつくる。 電気双極子とは分子どうしが近づくことによりそれぞれ正電荷と負電荷が存在する状態のことである。 すると、この２つの電気双極子のあいだにクーロンの法則に準じた相互作用がはたらくことになる。これがファン・デァ・ワールスの引力である。
しかし、分子どうしが近づきすぎると、それらは接触を避けるために強い斥力がはたらく。 こうして分子間にはたらく位置エネルギーは分子間の距離ｒの関数として図２に示されるようなかたちであらわされることになる。 すると、分子間の間隔ｒAであるとき、位置エネルギーは最小であり、このときがもっとも安定であるということになる。
さて、固体に外力を与えてひきのばすと分子は図のＢ点にうつり、位置エネルギーが大きくなり、不安定となる。 そうしてＡ点に戻ろうとする力がはたらく。これが弾性力である。
Ｂ点の位置ｒがｒAからあまり離れていないときには、図２の点線であらわしたように、近似的に位置エネルギーは放物線であらわすことができ、 その位置エネルギーＶは右の式(１)のように変位(ｒ－ｒA)との関係になる。 したがって、このとき分子間に作用する弾性力Ｆは、位置エネルギーを距離で微分することにより、式(２)としてあたえられる。 つまり弾性力は変位に比例するというフックの法則が成立する。この変形を弾性変形といい弾性力を固体断面積で割ったのものを弾性率という。 この説明からもわかるように変位(ｒ－ｒA)があまり大きいとフックの法則は成立しない。
このように固体の弾性力の原因の根本は分子間にはたらく引力にあり、 そのまた根本の原因は荷電粒子間(電気双極子)にはたらくクーロンの近接作用(電気的引力)にあるのである。

［参考文献］

1. 精構物理　学生社　砂川重信