株式会社ユービーエム
〒617-0004
京都府向日市鶏冠井町四ノ坪30-11
TEL：075-935-1006
FAX：075-935-2823
E-mail：jdm04354@nifty.com
技術的なお問い合わせ
カスタマーサービス電話
TEL：075-935-1008
〒617-0004
京都府向日市鶏冠井町四ノ坪30-11
TEL：075-935-1006
FAX：075-935-2823
E-mail：jdm04354@nifty.com
技術的なお問い合わせ
カスタマーサービス電話
TEL：075-935-1008
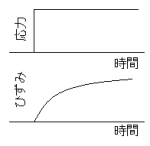
画物体に一定の応力を与えることによってひずみ(変形)が増加する過程。
粘弾性物体(高分子)は、右図のように一定応力を与えられ
た直後、ひずみの増加速度が高く、徐々に低くなりやがて
一定ひずみに集束する。
これは、応力を与えた後、物体の構造変化に影響する粘性と弾性の相互作用である。
・ひずみ＝物体の原形に対して変形させた量の比
(HOME基礎講座［1.粘弾性とは］図２参照 )
・クリープ詳細
(HOME基礎講座［2.クリープと応力緩和］本文参照)
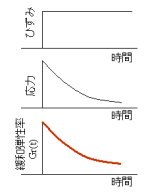
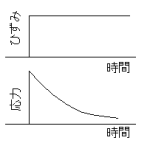画物体に一定のひずみを与えることによって生じた応力が減少する過程。
粘弾性物体(高分子)は、右図のように一定ひずみを与えら
れた瞬間に最大応力が生じ、直後応力の減少速度が高く、徐々にそれが低くなりやがて一定応力に集束する。
これは、ひずみを与えた後、物体の構造変化に影響する粘性と弾性の相互作用である。
・ひずみ＝物体の原形に対して変形させた量の比
(HOME基礎講座［1.粘弾性とは］図２参照 )
・応力緩和詳細
(HOME基礎講座［2.クリープと応力緩和］本文参照)
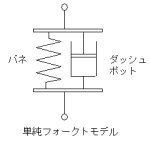弾性(バネ)と粘性(ダッシュポット)を１個づつ並列に連結した状態のモデル。図の上下両端を引っ張ると、弾性と粘
性に同一のひずみが生じ、応力がそれぞれに分散する構造
が特長。応力を規制したクリープの説明に適用する。
単純フォークトモデルを縦列に複数個連結したものが、一
般化フォークトモデルである。遅延スペクトルの説明に適
用する。
・クリープ詳細
(HOME基礎講座［2.クリープと応力緩和］本文参照)
・遅延スペクトル詳細
(HOME基礎講座［5.遅延スペクトルと応力緩和］本文参照)
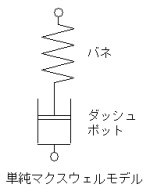弾性(バネ)と粘性(ダッシュポット)を１個づつ縦列に連結した状態のモデル。図の上下両端を引っ張ると、弾性と粘
性に同一の応力が生じ、ひずみがそれぞれに分散する構造
が特長。ひずみを規制した応力緩和の説明に適用する。
単純マクスウェルモデルを並列に複数個連結したものが、
一般化マクスウェルモデルである。緩和スペクトルの説明
に適用する。
・応力緩和詳細
(HOME基礎講座［2.クリープと応力緩和］本文参照)
・緩和スペクトル詳細
(HOME基礎講座［5.遅延スペクトルと応力緩和］本文参照)
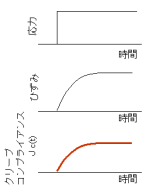物体に一定の応力を与えている間、ひずみが増加する過程(クリープ)のある時間におけるひずみを与えた応力
で割った値をクリープコンプライアンスＬc(t)［1/Pa］と
いう。(Ｌc(t)＝経過時間ｔにおけるひずみ/応力)
経過時間の間隔を短くとり、各時間毎にＬc(t)を求めると
右図のクリープコンプライアンス曲線を得る。
同曲線は高分子物体の粘性に対する弾性の寄与を評価するうえで有効である。
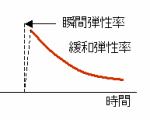
高分子物体に瞬時(時間0)にひずみを与えると、生じた応力は緩和する間がなく、全て物体の内部エネルギーになる。この瞬間の弾性率をいう。または完全弾性率という。
実際、瞬時にひずみを与えることは不可能であるため、瞬
間弾性率Ｇr(0)の実測はできない。
緩和弾性率曲線が１００％弾性からエネルギー放出成分の増加過程と考えると、同曲線から短時間の間隔に置ける、
全ての緩和弾性率を積算することにより近似的に瞬間弾性
率が求まるのである。
高分子物体に瞬時(時間0)にひずみを与えると、生じた応力は緩和する間がなく、全て物体の内部エネルギーになる。この瞬間の弾性率をいう。または完全弾性率という。
実際、瞬時にひずみを与えることは不可能であるため、瞬
間弾性率Ｇr(0)の実測はできない。
緩和弾性率曲線が１００％弾性からエネルギー放出成分の増加過程と考えると、同曲線から短時間の間隔に置ける、全ての緩和弾性率を積算することにより近似的に瞬間弾性
率が求まるのである。
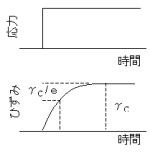高分子物体に一定応力を与えている間、ひずみが時間経過につれて二次曲線上に増加してゆき、やがて平衡になる。(クリープ)
ひずみの増加が平衡になる大きさよりも、その1/e(=1/2.7
2)小さいひずみまで増加したときの経過時間を遅延時間と
決める。
・遅延時間詳細
(HOME基礎講座［3.遅延時間と緩和時間］本文参照)
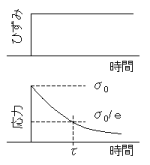高分子物体に一定ひずみを与えている間、応力が時間経過につれて減少する。(応力緩和)初期応力の1/e(=1/2.72)まで減少したときの経過時間を緩和時間τと決める。
・緩和時間詳細
(HOME基礎講座［3.遅延時間と緩和時間］本文参照)
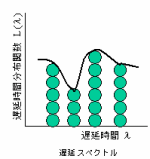高分子物体が多様の遅延時間をもつ分子鎖で構成されており、各遅延時間における分子鎖の数を遅延時間分布関数といい、遅延時間との関係を遅延スペクトルいう。縦軸単位はクリープコンプライアンスの1/Paで表記され、
数値は分子鎖の数を掛け合わせた緩和弾性率の逆数である。
・遅延時間詳細
(HOME基礎講座［3.遅延時間と緩和時間］本文参照)
・遅延スペクトル詳細
(HOME基礎講座［5.遅延スペクトルと緩和スペクトル］ 本文参照)
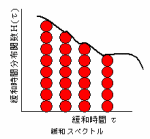高分子物体が多様の緩和時間をもつ分子鎖で構成されており、各緩和時間における分子鎖の数を緩和時間分布関数といい、緩和時間との関係を緩和スペクトルいう。縦軸単位は緩和弾性率のPaで表記され、数値は分子鎖の数を掛け合わせた緩和弾性率である。
・緩和時間詳細
(HOME基礎講座［3.遅延時間と緩和時間］本文参照)
・緩和スペクトル詳細
(HOME基礎講座［5.遅延スペクトルと緩和スペクトル］ 本文参照)
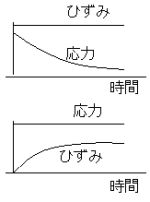高分子物体に初期応力を与え、その応力を一定に維持したままひずみの増加速度を測定するクリープ測定。高分子物体に初期ひずみを与え、そのひずみを一定に維持したまま応力の減少速度を測定する応力緩和測定。
・応力緩和・クリープ詳細
(HOME基礎講座［2.遅延時間と緩和時間］本文参照)
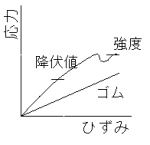短冊状の試料を一定速度で伸張させる過程における応力とひずみの関係をいう。一般的に引っ張り試験で時間経過に伴う応力とひずみの関係である。狙いは固体の降伏値と強度、あるいはゴム弾性(架橋密度)に基づくひずみの大きさなどを知ることである。
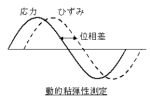高分子物体に正弦波応力を与えることにより、物体の応答として正弦波ひずみが生じる。両者の比と位相差から生じたエネルギーを高分子物体の内部エネルギーと熱エネルギーに分けることができる。前者を弾性、後者を粘性と称し、高分子物体がそれらの共存であることを知り、その状態が温度や時間に依存することから物体の内部構造を予測する手法である。・詳細
(HOME基礎講座［6.動的粘弾性測定］本文参照)
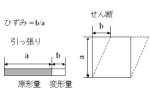物体が外力を受けて生じた変形と受けるまえの原形との比。物体が長さ方向に力をうけて生じたひずみは同方向の変形と元の長さとの比。
物体の長さに対して法線方向に力を受けて生じたひずみは、法線方向に生じた変位と元の長さとの比。
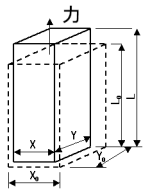物体に外力を与えるとひずみ(変形)が生じる。生じるひずみは、力の方向と法線方向の二成分である。
法線方向のひずみと力の方向のひずみの比をポアソン比という。
力の方向のひずみ 法線方向のひずみ
εL＝(L-L0)/L0 εX＝(X-X0)/X0 εY＝(Y-Y0)/Y0
ポアソン比
μX＝-εX/εL μY＝-εY/εL μX=μY
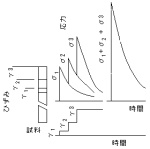試料に微小ひずみγ1、γ2、γ3を階段状に与えてやると、それぞれのひずみに対する応力σ1、σ2、σ3は独立して
増加する。この繰り返しひずみによる応力の増加をボル
ツマンの重畳原理という。
ひずみγ1+γ2+γ3を与えた初期応力はσ1＋σ2＋σ3が
成立する。
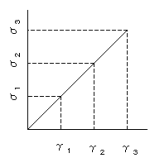物体に与える応力σとひずみγの関係が比例する場合、各応力σ１σ２σ３に対応するひずみγ１γ２γ３との関係から求まる弾性率は一定である。これを線形弾性率という。
弾性率＝応力/ひずみ
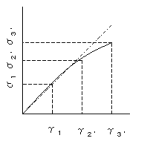物体に与える応力σとひずみγの関係が比例しない場合、各応力σ１σ２'σ３'に対応するひずみγ１γ２'γ３'との関係から求まる弾性率はそれぞれ異なった値である。
これを非線形弾性率という。
Ｄｙｎａｍｉｃ
Ｖｉｓｃｏｅｌａｓｔｉｃｉｔｙ
Ｍｅａｓｕｒｉｎｇ Ａｐｐａｒａｔｕｓ
：動的粘弾性率測定装置
Ａｐｐａｒａｔｕｓ for Ｍｅａｓｕｒｉｎｇ
Ｄｙｎａｍｉｃ Ｖｉｓｃｏｅｌａｓｔｉｃｉｔｙ
：動的粘弾性率測定装置
Ｍｅａｓｕｒｉｎｇ Ａｐｐａｒａｔｕｓ
：動的粘弾性率測定装置
Ａｐｐａｒａｔｕｓ for Ｍｅａｓｕｒｉｎｇ
Ｄｙｎａｍｉｃ Ｖｉｓｃｏｅｌａｓｔｉｃｉｔｙ
：動的粘弾性率測定装置
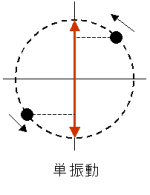１秒間に往復する回数。単位：Hz(=1/sec)周期(sec)＝1/周波数 １往復に要する時間。
周波数×２π(3.14) 単位：rad/sec
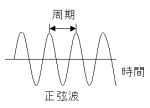質点が円周上を一定速度(角速度)で移動するとともに、縦軸上の変位として反映する。変位の履歴を時間軸上に
描いた波形。
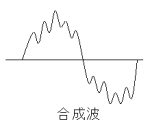ひとつの波にはひとつの周期がある。複数の波には複数の周期がある。複数の波が同時に生じた場合、周期の異
なる波どうしが重なって新しいかたちの波が生じる。
これを合成波という。
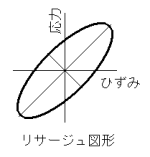物体に動的応力を与えると動的ひずみが生じる。１周期(往復)の応力とひずみの関係を二次元座標に描
いた図形をいう。応力に対してひずみの遅れ(位相差)
が大きいほど楕円の短長軸比が１に近い。位相差が小さ
いほど０に近い。粘弾性体は位相差が0.5付近である。
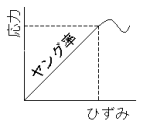物体を長さ方向に一定速度で引っ張ると応力とひずみがそれぞれ大きくなり続ける。応力とひずみが比例する範囲内における両者の関係をいう。ヤング率(Pa)＝応力/ひずみ
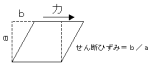物体の縦に対して横方向に応力を与える(せん断応力)と横方向に変形が生じる。縦の長さと横の変形との比を
せん断ひずみといい、せん断応力との比をせん断弾性率
という。
せん断弾性率(Pa)＝せん断応力/せん断ひずみ
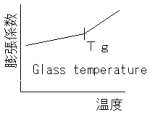固体の高分子物体を加熱し、物体の温度が上昇すると膨張する。ある温度まで膨張率は一定であるが、ある温度
で膨張率が変化して大きくなる。その温度をいう。
ガラス転移温度以下で高分子物体に動的外力を与えると
殆ど内部エネルギーになり、ガラス転移温度以上では、
同エネルギーと熱エネルギーが共存する。
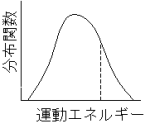物体内部は分子の運動エネルギーの大きさが幅広く分布しており、ある大きさの運動エネルギーを超えると、分子の反応が生じる。
分子の反応に寄与するエネルギーの大きさをいう。
活性化エネルギーが低いほど、物体内部における反応分
子の割合が多くなるため物体(分子の集合体)の反応が
速い。活性化エネルギーは物体の反応速度の係数である。
活性化エネルギーの求め方のことをいう。活性化エネルギーは反応速度の係数であるので、右の
反応速度式における左辺と右辺の1/Tとの関係が活性化
エネルギーである。動的粘弾性測定から求める場合は
ガラス転移温度が測定周波数に依存することから、
周波数と1/ガラス転移絶対温度との関係をとる。
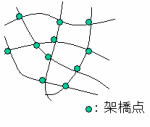架橋ゴムの単位体積あたりに存在する架橋点数。単位はmol/cc。この場合のmolは物体に外力を与えるこ
とにより生じる単位体積当たりの内部エネルギー(Joule
/cm3)と気体定数(8.31Joule/k.mol)*温度(k)との関係
により求まる架橋点分子の数である。内部エネルギーは
架橋点数に関係する。
２種類以上の物質が反応し別の物質が生成した場合の、反応と非反応の割合をいう。反応の割合が多いほど、
生成物の性質が顕著に現れ、反応前の物質や非反応成分の性質が現れる傾向が低下する。
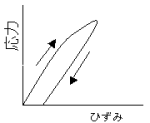外力を与え変形した物体から、与えた外力を取り除いた後、原形に戻らない性質をいう。戻る性質を弾性という。