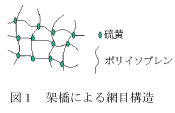
天然ゴムはイソプレンCH2=C(CH3）CH=CH2を主成分とする鎖状高分子ポリイソプレンである。 これに硫黄S2を混入（加硫）し加熱すると硫黄がポリイソプレン間をつなぐ役割をする。 このつなぎ目を架橋という。
　熱加硫した天然ゴムは数多くの架橋点により３次元の網目構造をつくり、 架橋点の数量が網目の大きさに逆比例する。生ゴムの繰り返し単位(単位体積)あたりに存在する架橋点数を架橋密度という。 網目が大きいほど架橋密度は低く、架橋点間のイソプレン分子量は大きい。天然ゴムの内部構造は各分子鎖が縮んだ状態をしているため、 外部から引っ張ると架橋密度が低い（網目が大きい）ほど伸びる変位（ひずみ）が大きい。

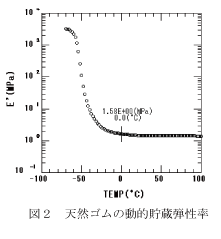　図２は天然ゴムの動的貯蔵弾性率の温度依存性である。
-30℃付近からの平坦な曲線はゴム内部が図１のように網目構造であることに相当する。
-70℃付近の高いE’は凝集したゴム内部の分子鎖どうしが絡み合った状態にあり、 外部から引っ張ると単位ひずみに対して大きな応力が生じることに相当する。
昇温に伴いE’の急激な低下は、ゴムのガラス転移に相当し、絡み合った分子鎖の解れ過程である。
解れた後ゴム内部には熱加硫による架橋構造が残り図１の状態（実際には３次元網目構造）で温度軸に対して平坦なゴム弾性率曲線になる。
（前節　架橋ゴム参照）

　架橋ゴムの弾性は架橋密度と相関（上記）するため、動的貯蔵ゴム弾性率と測定温度から架橋密度ｎ（mol/cc）が求まる。 また架橋密度の逆数１/ｎを架橋指数と言いい、架橋点間のポリイソプレン分子量に相当する。
右の関係式を使って図２の天然ゴム0℃における架橋密度を求める手順は下記の通りである。
1）単位を揃える
　E’=1.58（MPa）=1.58E+07（dyn/cm2）　…（1）
　R=8.31（J/mol・k）=8.31E+07（dyne・cm/mol・k）　…（2）
　T=0(℃)=273（k）　…（3）
2)(1)～(3)それぞれ右の関係式に代入する。
　ｎ=1.58E+07（dyne/cm2）
　　　/3*8.31E+07（dyne・cm/mol・k）・273（k）
　　=2.32E-04（mol/cm3）
　　=2.32E-04（mol/cc）　　＊1cm3=1CC
上記ｎは単位体積あたりに存在する架橋分子（この場合硫黄S2）の数である。（1mol=6.02E+23個：アボガドロ数）高分子のポアソン比の関係上、 引っ張り弾性率(Ｅ’)＝せん断弾性率(３Ｇ’)であることから、動的せん断弾性率と架橋密度の関係はｎ＝Ｇ’/ＲＴである。

［参考文献］

1. レオロジーなんかこわくない！　―　数式のないレオロジー入門　―
   （サイエンス＆テクノロジー発行　上田　隆宣　著）
   第六章　典型的な粘弾性変形
   
   
2. 架橋の物理化学
   （特集ゴムと架橋　西　俊夫　著）